Retos 300
Cantidades en perspectiva
Claudia Hernández

El famoso juego del ajedrez tiene asociada una leyenda bastante conocida que va más o menos así: un rey muy afligido por la muerte de su hijo en batalla ofreció riquezas a quien pudiera levantarle el ánimo. Un joven le presentó un tablero a cuadros y le explicó cómo jugar ese juego de estrategia, que le hizo entender que a veces es necesario el sacrificio de algunas piezas (como pasó con su hijo) para conseguir el fin último (proteger la corona). Agradecido, el rey le ofreció al joven lo que quisiera y éste sólo pidió granos de trigo, contabilizados de la siguiente manera: 1 grano por la primera casilla, 2 granos por la segunda, 4 granos por la tercera, 8 por la cuarta, y así duplicando la cantidad hasta llegar a la casilla 64. Ofendido, el rey pidió a sus asesores que le entregaran el costal que estaba pidiendo, pero los asesores pronto se dieron cuenta de que sus reservas de trigo no alcanzaban ni alcanzarían jamás para pagarle al joven lo que pedía.
El último de la fila
Para saber de cuántos granos estamos hablando podemos representarlos con esta suma de números: 1 + 2 + 4 + 8 + …, que también puede escribirse como suma de potencias de 2: 20 + 21 + 22 + 23 … Si el tablero tiene 64 casillas, ¿qué potencia de 2 corresponde al último sumando? Piénsalo bien porque la intuición luego nos engaña.
En costales
Cuando escribimos el resultado de la pregunta anterior sumando como un número con todos sus dígitos vemos que es enorme: 9 223 372 036 854 775 808. Y si a éste le sumamos lo de las otras 63 casillas, podemos comprobar que la cantidad de granos de trigo que el joven estaba pidiendo es igual a 18 446 744 073 709 551 615. ¿Cómo harías para calcular la cantidad de costales que se necesitan para almacenar todos esos granos de trigo? No es necesario que la calcules, el simple ejercicio de imaginación es reto suficiente.
Misión imposible
Ah, pero la historia termina en que se trataba de una cantidad de trigo inmensa y que no podrían dársela nunca. El último reto viene en dos partes. La primera es que te aventures a hacer una estimación de cuántos años de cosecha mundial equivalen a la cantidad de trigo que el joven pidió, así, a ojo de buen cubero. La segunda es que averigües si estuviste en lo correcto, y para ello va un poco de ayuda con dos pistas: 1) 100 granos de trigo pesan aproximadamente 5 gramos, o sea que en 1 kilo hay como 20 mil granos de trigo; 2) según la fao, la producción mundial de trigo para el 2022 fue de casi 800 millones de toneladas.
Si quieres saber más sobre ajedrez échale ojo a nuestra Guía del maestro: https://www.comoves.unam.mx/assets/revista/20/guiadelmaestro_20.pdf.
Soluciones núm. 299
Diferente acercamiento
El máximo número de regiones en que se divide el círculo con 3 segmentos es 7. Con un segmento podemos dividirlo en máximo 2 regiones y con 2 segmentos lo dividimos en máximo 4. No hay manera de que el tercer segmento corte estas 4 regiones, pero sí 3, y por eso el máximo número de regiones es 7 (la región que queda intacta más las 6 que se obtienen de cortar las otras 3).
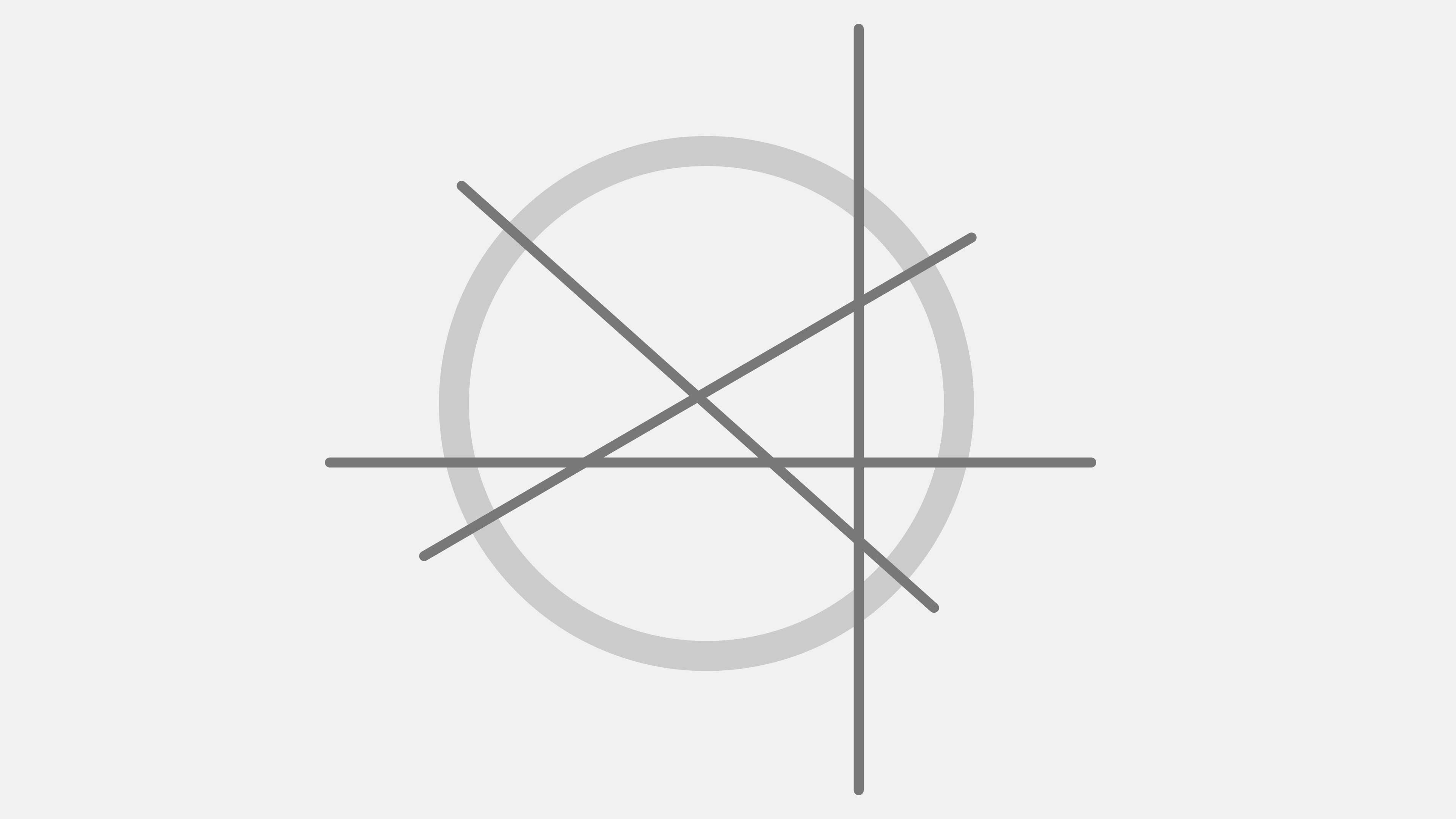
Encontrar similitudes
Ésta es una forma de dividir el círculo y la luna en 4 regiones con 2 segmentos de recta:


Reconocer diferencias
Con 2 segmentos de recta el círculo se puede dividir en un máximo de 4 regiones, pero para la luna el máximo es 6. El secreto está en que una forma es convexa y la otra no.















