Retos 307
Ordena por aquí y por allá
Claudia Hernández García

Ilustración: Santiago Solís Montes de Oca
Ordenar es una operación básica del pensamiento matemático que siempre ponemos en práctica, aunque rara vez nos detenemos a pensar en qué consiste el proceso; sólo lo llevamos a cabo y ya. Antes de seguir leyendo les propongo que traten de definirlo con sus propias palabras.
De a dos
Cuando ordenamos un conjunto de elementos lo que hacemos es compararlos de dos en dos para darles una secuencia y definir cuál va antes y cuál va después. A veces el criterio que elegimos tiene un consenso colectivo, como al ordenar números de menor a mayor, pero en otras ocasiones hay que explicar nuestra lógica y quizá alguien no esté de acuerdo con el acomodo. El primer reto consiste en ordenar las siguientes imágenes de dos maneras distintas, una en la que todas las personas podríamos estar de acuerdo y una que sea más bien subjetiva (y explicar por qué, claro).

Todas las que hay
Estas formas de ordenar son apenas dos de las muchas posibles. ¿Podrías adivinar cuántas hay en total? El segundo reto no consiste en estimar esta cantidad, sino en encontrar todas las formas en las que se pueden ordenar cuatro de esas pinturas. ¿Por qué cuatro? Porque es una cantidad de opciones más manejable que si lo hacemos con las cinco.
Condición adicional
Matemáticamente hablando, lo que acabamos de hacer es encontrar las permutaciones de un conjunto de cuatro elementos; se trata de una forma de conteo que se estudia en análisis combinatorio. Para el último reto vamos a hacer otro ejercicio de permutar, pero con un desafío extra. Piensa en todos los números de tres cifras y encuentra los múltiplos de cuatro que cumplen la propiedad de que cualquier permutación de sus dígitos también es múltiplo de cuatro. Por ejemplo… 244 es un múltiplo de 4 y 424 también lo es, pero 442 no; entonces no cumplen la condición. En cambio, 444 sí la cumple, porque todas las permutaciones dan el mismo número múltiplo de cuatro.
El término ordenar tiene otros usos, pero los dejaremos para después. ¡Felices retos!
Soluciones núm. 306
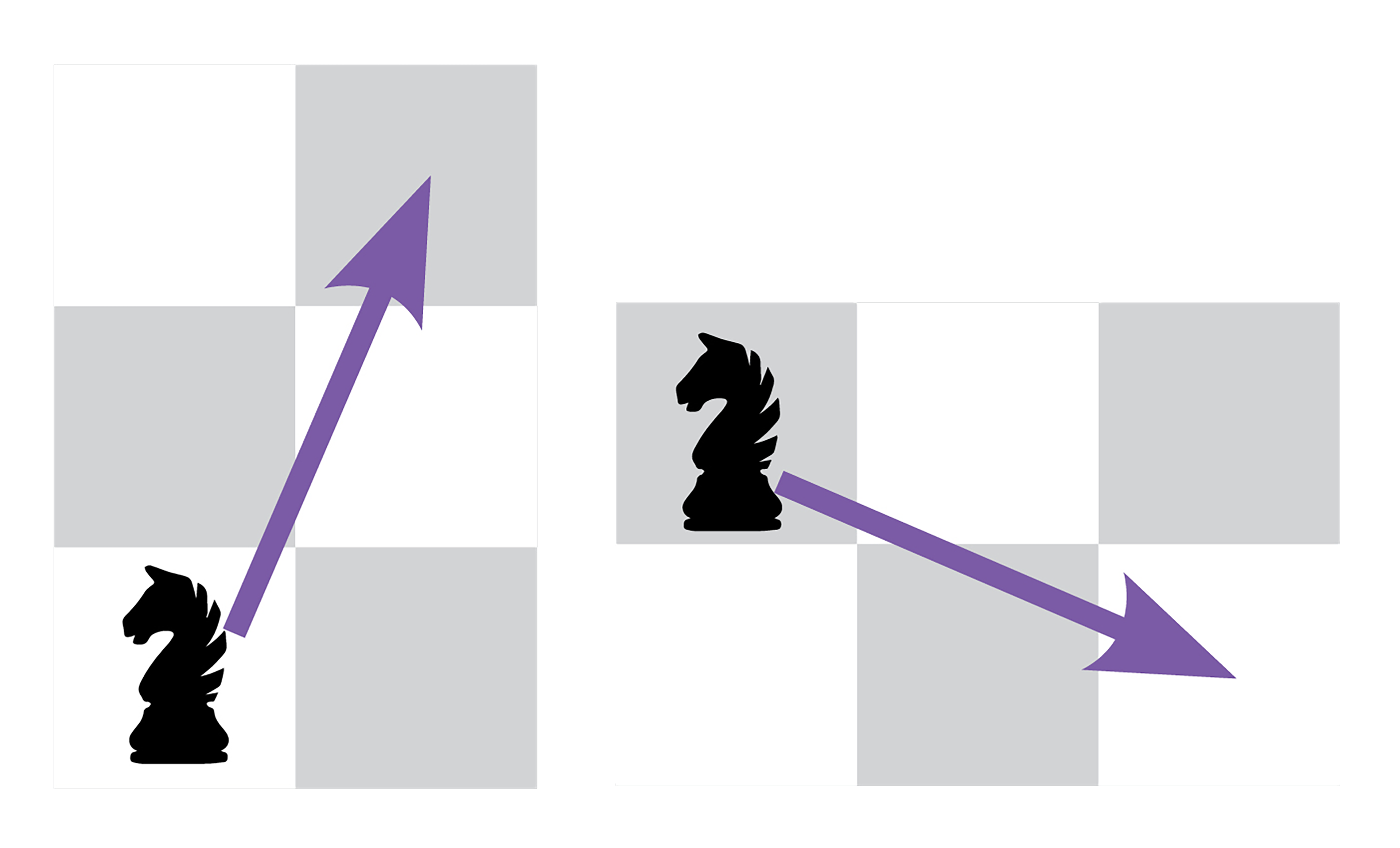
Tu propio teorema. El caballo siempre va a llegar a un cuadro de un color distinto al del que salió porque siempre se mueve por la diagonal de un rectángulo que tiene contraesquinas de colores diferentes: si parte de uno blanco llega a uno negro y viceversa.
Dos soluciones. El recorrido de Euler es abierto, o sea que no termina donde empezó; primero recorre una mitad del tablero y luego la otra; la diferencia entre los números simétricamente opuestos siempre es 32. El recorrido de Beverley es un circuito; todas las filas y las columnas del cuadrado completo suman 260 y todas las de los cuadrantes suman 130.
Atacar a nadie. Los 32 caballos se colocan en todos los cuadrados de un mismo color.