Retos 308
Acomodo cuadricular
Claudia Hernández García

Ilustración: Santiago Solís Montes de Oca
Una de las personas que más trabajó en el planteamiento y la resolución de problemas fue el matemático húngaro George Pólya (1887-1985). En el prefacio de su libro Cómo plantear y resolver problemas menciona que en la solución de todo problema hay un cierto descubrimiento y que si se resuelve por métodos propios se puede experimentar el goce del triunfo.
Además de sugerir heurísticas para resolver problemas de todo tipo —no sólo matemáticos—, también propuso estrategias para enseñar y aprender a encontrarlas. Si les suena familiar la palabra heurística (técnica de la indagación y del descubrimiento) es porque proviene de la expresión arquimedeana eureka, de la cual hablamos en “Pensar fuera de la caja”, en ¿Cómo ves?, núm. 299. Les propongo que vayamos, pues, con los retos de esta ocasión y tengamos un momento eureka.
De una en una
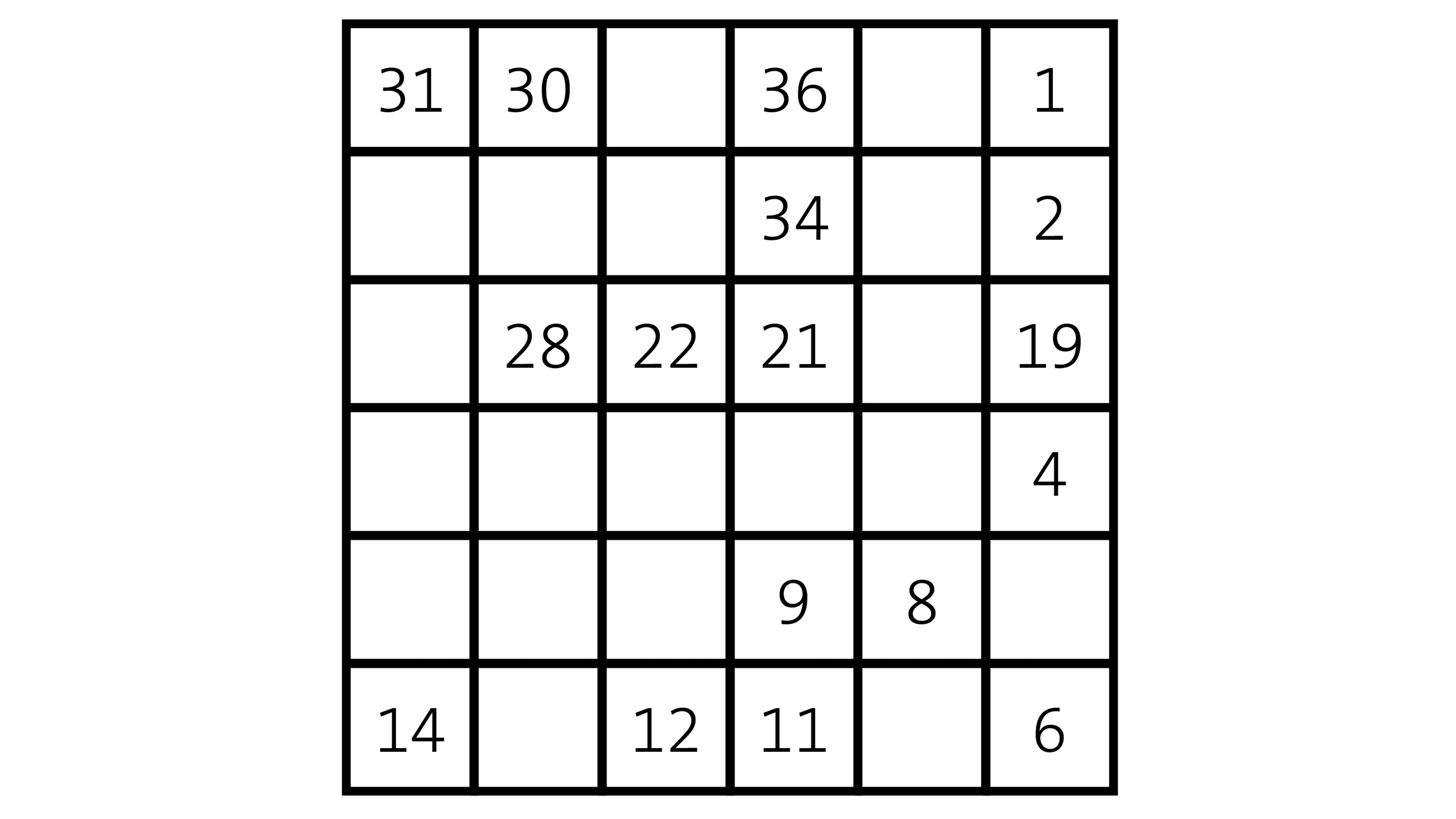
El primer reto consiste en acomodar los números del 1 al 36 en la siguiente cuadrícula. Para hacerlo hay que ir colocando los números en orden consecutivo mientras recorren las casillas de forma horizontal, vertical o diagonal, una a la vez. Entre cualquier número y su antecesor o sucesor debe haber una sola casilla de distancia.
Que no queden juntas
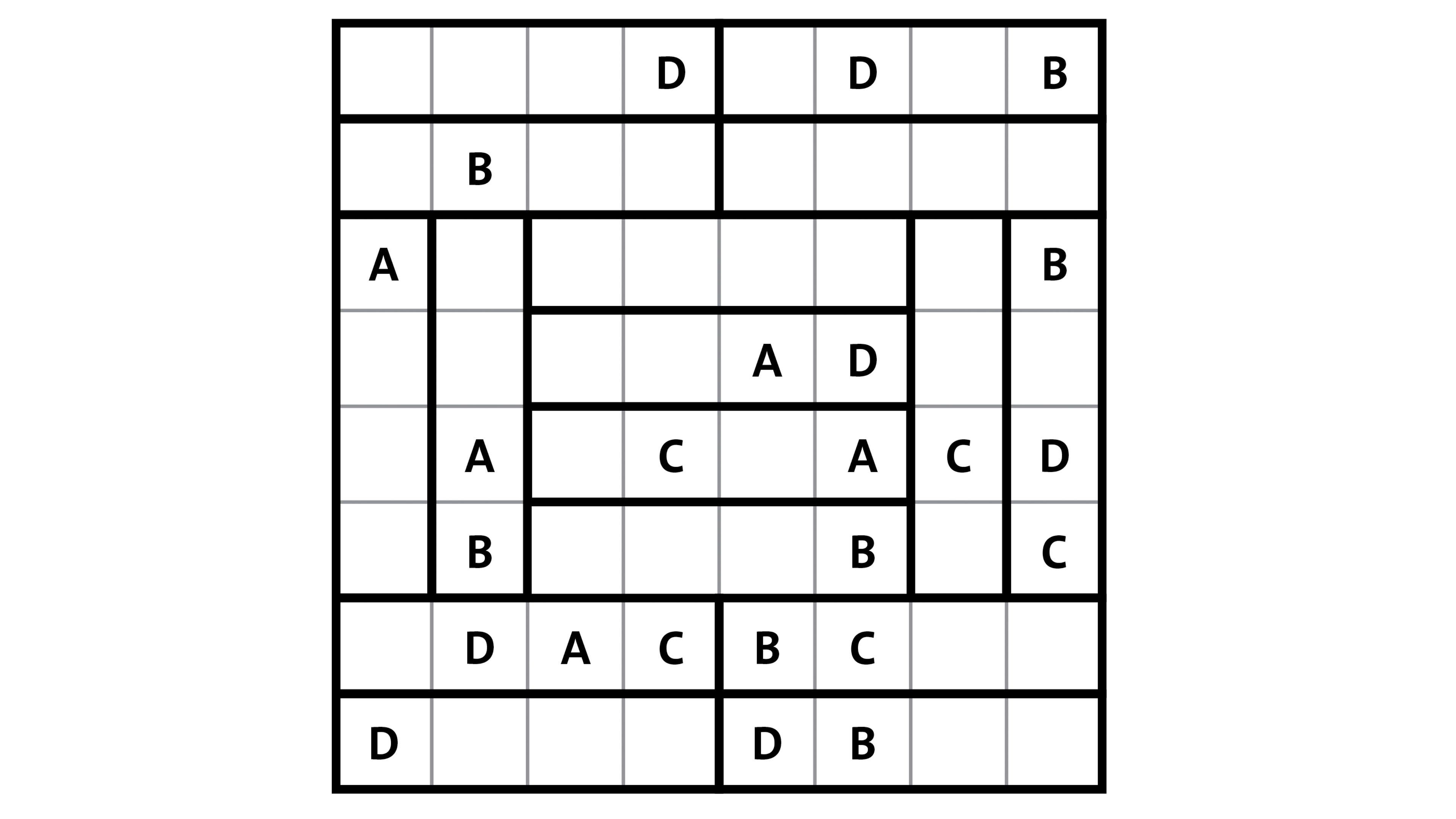
Ahora hay que colocar las letras A, B, C y D en el tablero, con las siguientes tres reglas: 1) cada región delimitada por líneas oscuras debe contener cuatro letras diferentes, 2) los cuadrados que comparten un lado no pueden tener la misma letra y 3) todas las filas y columnas deben contener exactamente dos tantos de cada letra.
Tripletas prohibidas
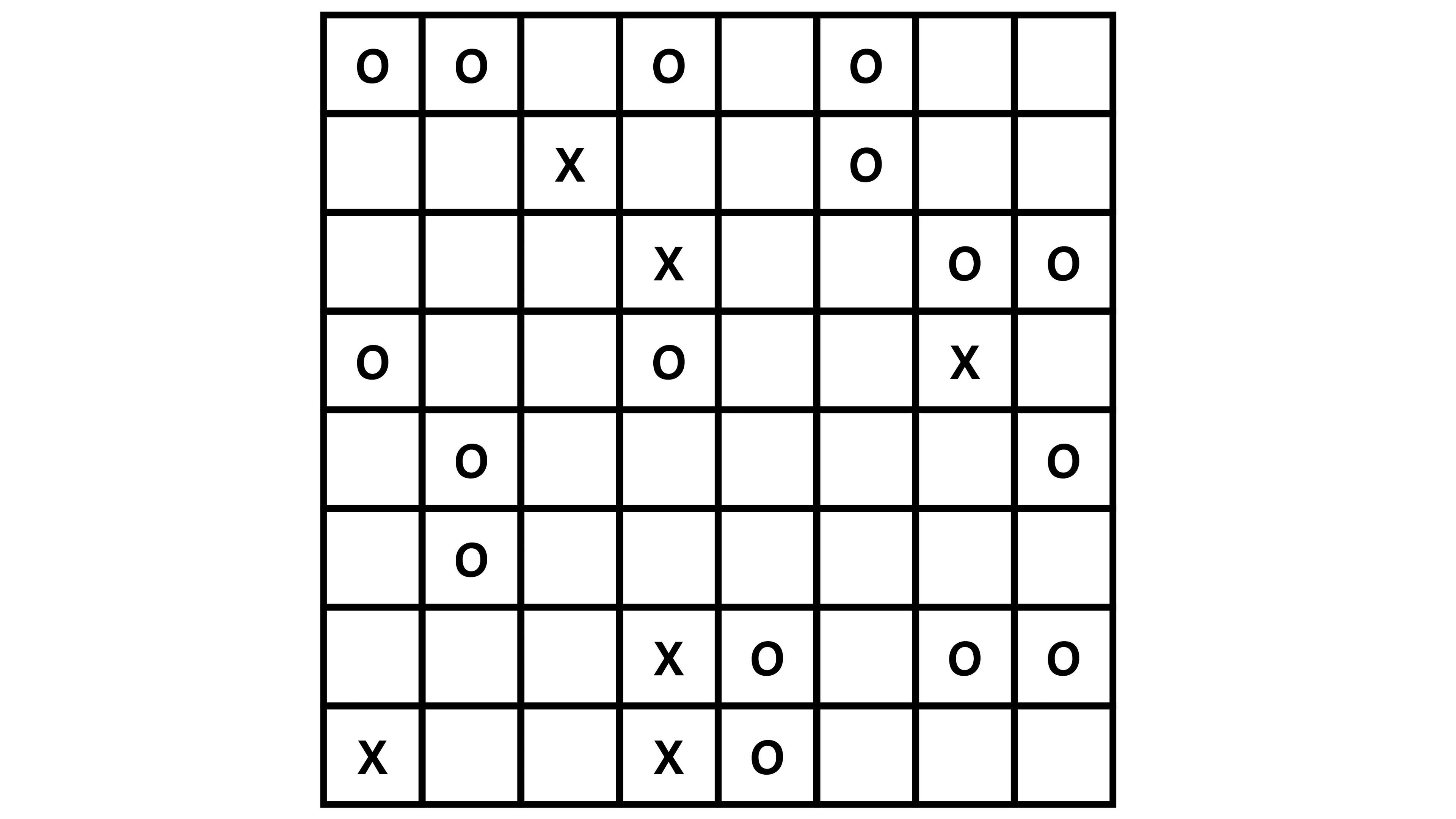
Finalmente hay que llenar este tablero de círculos y taches cuidando que no queden tres cuadrados consecutivos en línea con el mismo símbolo y que al final haya la misma cantidad de taches y círculos en cada fila y en cada columna.
¡Felices retos!
Soluciones núm. 307
De a dos. Un acomodo que da poco margen a la objeción es el orden cronológico ascendente: 2-4-1-5-3. Un criterio subjetivo es ordenarlas de la que nos gusta más a la que nos gusta menos, y pues aquí hay más posibilidad de conversación.
Todas las que hay. La cantidad de permutaciones posibles de las cinco pinturas es 120. Las permutaciones de sólo cuatro de ellas son 24: 1 234, 1 243, 1 324, 1 342, 1 423, 1 432, 2 134, 2 143, 2 314, 2 341, 2 413, 2 431, 3 124, 3 142, 3 214, 3 241, 3 412, 3 421, 4 123, 4 132, 4 213, 4 231, 4 312 y 4 321.
Condición adicional. Los números que cumplen las condiciones son 444, 448, 484, 488, 844, 848, 884 y 888.